
Das ZYBO ist nun bereits in der Lage Audiodateien in Form von Wave-Dateien von einer SD-Karte auszulesen und diese mit Hilfe des vorhandenen SSM2603 Audiocodecs auf einem Lautsprecher auszugeben. Nun soll die Kette um einen digitalen Filter erweitert werden, sodass das Audiosignal in Hardware bearbeitet und störende Komponenten im Signal entfernt werden können.
Bevor ich auf das Design des Filters eingehe, wird eine entsprechende Audiodatei benötigt. Entsprechende Wave-Dateien können in Python mit dem Modul wavio erstellt werden. Ein entsprechendes Python-Skript kann in meinem GitHub-Repository heruntergeladen werden.
import math
import wavio
import argparse
import numpy as np
import matplotlib.pyplot as plot
def LevelType(x):
x = float(x)
if(x > 0.0):
raise argparse.ArgumentTypeError("Maximum audio level is 0 dBFs!")
return x
Parser = argparse.ArgumentParser()
Parser.add_argument("-n", "--name", help = "Output file", type = str, default = "Sample.wav")
Parser.add_argument("-f", "--freq", help = "Comma separated list with signal frequencies", type = str, default = "1000.0")
Parser.add_argument("-fs", "--sample", help = "Sampling frequency", type = int, default = 48000)
Parser.add_argument("-l", "--level", help = "Audio level in dbFs", type = LevelType, default = 0.0)
Parser.add_argument("-t", "--time", help = "Signal length in seconds", type = int, default = 3)
args = Parser.parse_args()
Amplitude = 1.0
if(__name__ == "__main__"):
Gain = math.pow(10, args.level / 20)
Frequencies = args.freq.replace(" ", "").split(",")
try:
Frequencies = [float(i) for i in Frequencies]
except ValueError:
print("[ERROR] Invalid frequency!")
exit()
Signal = Amplitude * Gain
t = np.linspace(0, args.time, args.time * args.sample, endpoint = False)
for Freq in Frequencies:
Signal = np.multiply(Signal, np.sin(2 * np.pi * float(Freq) * t))
plot.plot(t[0:int(args.sample / min(Frequencies))], Signal[0:int(args.sample / min(Frequencies))])
plot.title("Output signal")
plot.xlabel("Time [s]")
plot.ylabel("Amplitude")
plot.grid(True, which = "both")
plot.axhline(y = 0, color = "k")
plot.show()
wavio.write(file = args.name, data = Signal, rate = args.sample, scale = (-Amplitude, Amplitude), sampwidth = 2)
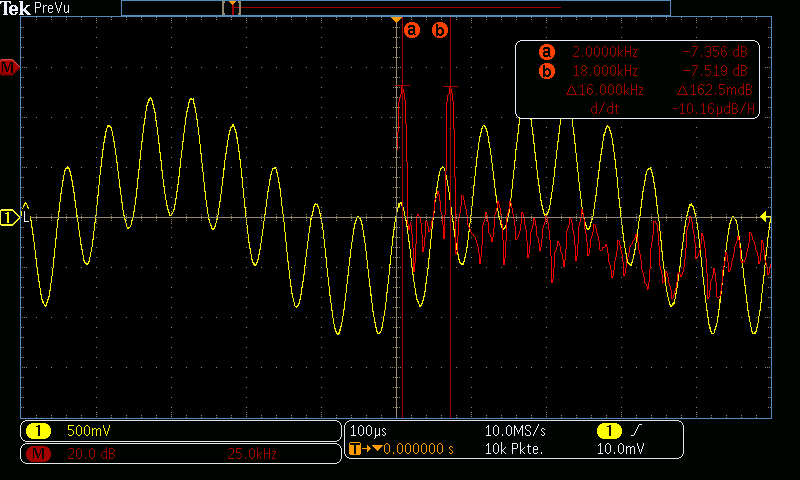
In diesem Beispiel soll ein digitales Tiefpass-Filter entworfen werden, welches Signale mit einem bestimmten Frequenzbereich aus den Audiodaten entfernt. Als Eingangssignal soll ein 2 kHz Sinussignal verwendet werden. Diesem Eingangssignal ist ein 18 kHz Störsignal überlagert und das komplette Signal ist mit einer Frequenz von 48 kHz abgetastet worden.
Die Umsetzung des Filters soll in C mit Hilfe der Vivado High-Level Synthesis vorgenommen werden, wobei der Filter mit Hilfe des Online-Tools MicroModeler DSP entworfen dimensioniert wird.
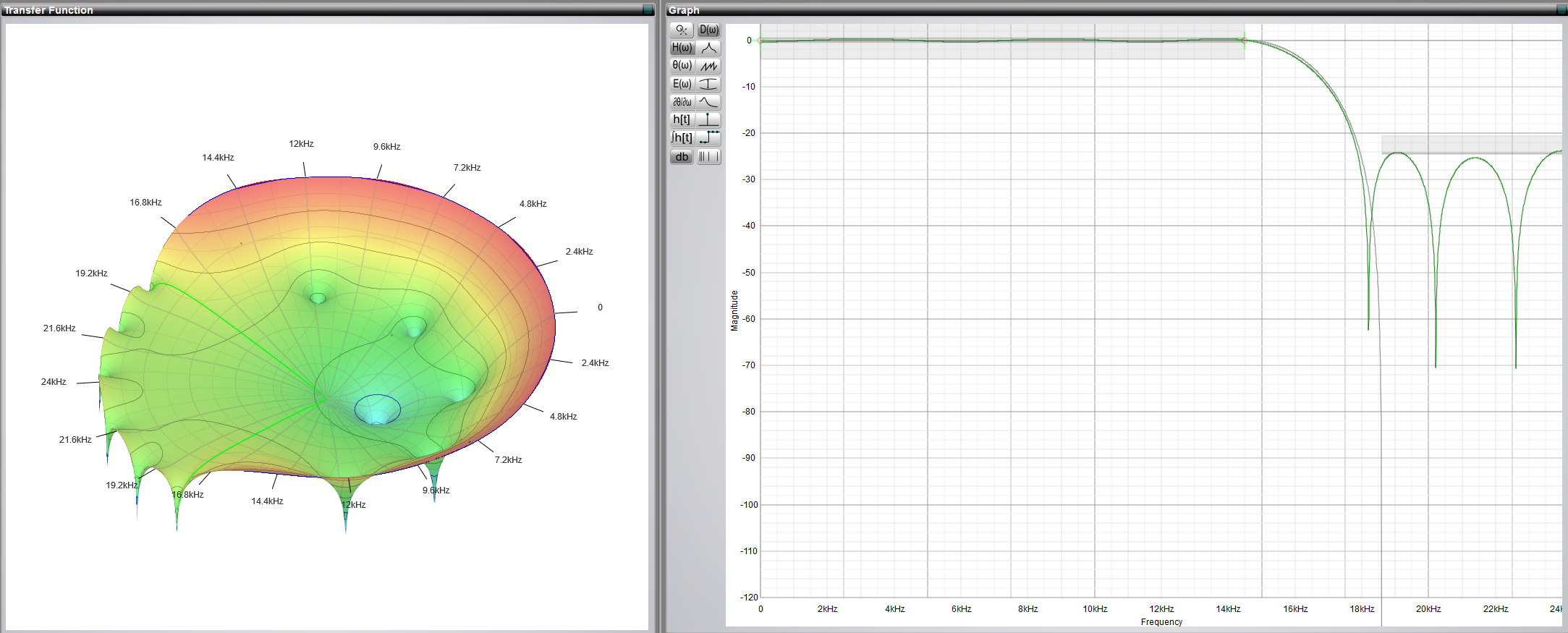
Dazu kann auf einen bereits entworfenen Low Pass Standardfilter zurückgegriffen werden, wobei die Länge des Filters auf 19 und die Grenzfrequenz, also die Frequenz bei der die Verstärkung um -3 dB (Faktor 0,5) gesunken ist, auf 16 kHz gesetzt werden. Es ergibt sich eine Verstärkung von etwa -30 dB (Faktor 0,001) für Frequenzen ab 18 kHz.
Der MicroModeler berechnet aus den gegebenen Parametern und den Null- bzw. Polstellen die Koeffizienten für den Filter. Diese können direkt aus dem erzeugten C-Code kopiert werden. Der MicroModeler erzeugt immer Arrays, deren Größe ein Vielfaches von 4 ist und ggf. mit 0,0 aufgefüllt werden. Diese Koeffizienten können ausgelassen werden.
Hinweis:
Der C-Code ist in diesem Beispiel leider unbrauchbar, da er sich nicht mit der Vivado HLS synthetisieren lässt. Daher sind nur die Koeffizienten von Interesse.
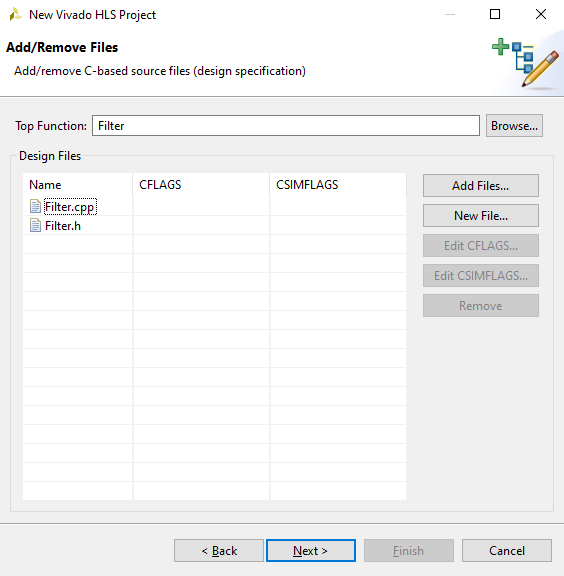
In Vivado HLS wird nun ein neues Projekt für den Filter angelegt und die Dateien für den C++-Code erstellt:
Im C++-Code wird dann eine Funktion namens Filter mit zwei Parametern erstellt. Diese Funktion dient als Top-Level Funktion, sprich es handelt sich um den Einstiegspunkt der High-Level Synthese.
Ein- und Ausgangssignale werden in der High-Level Synthese als Funktionsparameter dargestellt. Diese Signale können dann zusätzlich noch mit einem definierten Interface (z. B. AXI-Stream) versehen werden. Ausgangssignale, die auf einen Bus führen, werden als Zeiger dargestellt. Zudem wird in der High-Level Synthese ein int automatisch mit 32-Bit dargestellt, weshalb ein int den idealen Datentyp für dieses Szenario darstellt.
void Filter(int DataIn, int* DataOut, bool Enable)
{
}
Hinweis:
Der Parameter return wird auch von der HLS genutzt, wenn kein return im Code verwendet wird.
Alle Audiodaten sollen mit je einem DSP-Kern pro Kanal und in Festkommaarithmetik berechnet werden. Die DSP-Kerne in dem verwendeten Zynq-7000 sind von Typ DSP48E1 und besitzen je einen 25- und 18-Bit Eingang, einen 25-Bit Preadder, sowie einen 48-Bit Ausgang. Für die Berechnungen werden eigene Datentypen genutzt, die für den DSP optimiert sind und eine passende Länge aufweisen. Die Definition solcher Datentypen erfolgt mit Hilfe der Bibliothek <ap_fixed.h>.
typedef ap_fixed<16, 16> data_t; typedef ap_fixed<18, 1> coef_t; typedef ap_fixed<48, 16> acc_t; typedef ap_fixed<25, 16> sum_t;
Bei der Definition der Datentypen wird eine Gesamtlänge, sowie die Länge des ganzzahligen Teils der Zahl angegeben. Der Datentyp data_t ist somit insgesamt 16-Bit lang, wobei alle 16-Bit für den ganzzahligen Teil genutzt werden. Dieser Datentyp soll für die Audiodaten genutzt werden.
Der Datentyp acc_t ist 48-Bit breit und verwendet 16-Bit für den ganzzahligen Bereich. Es stehen somit bis zu 32-Bit für den gebrochenen Teil zur Verfügung. Dieser Datentyp wird für den Ausgang des DSP-Kerns genutzt und beinhaltet am Ende das Ergebnis der Operation.
Bei dem Datentyp coef_t handelt es sich um einen Datentyp für die Filterkoeffizienten. Dieser Datentyp ist 18-Bit breit, wobei der gebrochene Teil 17-Bit lang ist. Für den ganzzahligen Teil bleibt somit 1 Bit übrigt. Da alle Filterkoeffizienten kleiner als 1 sind, ist diese Aufteilung ideal und es lassen sich möglichst viele Stellen abspeichern.
Der letzte Datentyp ist der Datentyp sum_t. Dieser kann bei Bedarf für den Preadder des DSP-Kerns genutzt werden.
Achtung:
Werden negative Werte verwendet, so muss ein zusätzliches Bit für das Vorzeichen berücksichtigt werden! Zudem muss darauf geachtet werden, dass die verwendeten Werte nicht zu groß für den Wertebereich des Datentyps sind. So kann der Datentyp coef_t nur maximal 218 – 1 Werte darstellen. Wenn zusätzlich noch ein Vorzeichen genutzt und 17-Bit für den gebrochenen Teil verwendet werden sollen, ergibt sich ein maximaler Wertebereich von ~±0,99999237060546875.
![]()
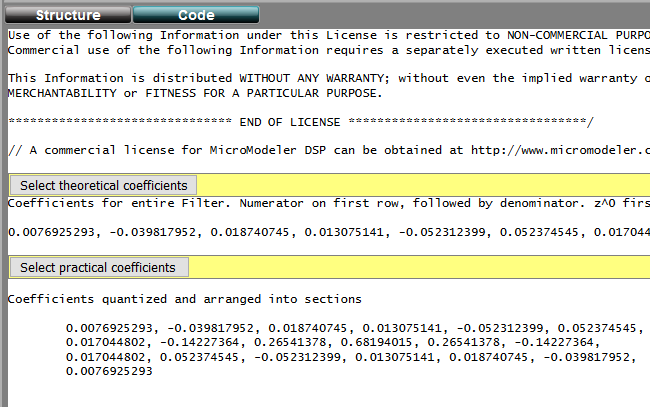
Die berechneten Filterkoeffizienten können direkt aus dem Designer herauskopiert werden, indem unter Code Generation → Tools der Punkt Data Export ausgewählt und zum aktuellen Projekt hinzugefügt wird. Über das entsprechende Menü kann das Ausgabeformat (z. B. CSV) ausgewählt werden. Die formatierten Koeffizienten können dann direkt aus dem Reiter Code herauskopiert werden.
In der HLS besteht die Möglichkeit die Koeffizienten über ein separates Interface einzuspeisen oder sie direkt in den Code zu integrieren. In diesem Beispiel sollen die Koeffizienten direkt in den Code integriert werden, was zwar etwas Speicher benötigt, aber dafür wird keine zusätzliche Schnittstelle benötigt. Für die Koeffizienten wird ein Array vom Typ coef_t verwendet:
static coef_t Coefficients[] = {
0.0076925293, -0.039817952, 0.018740745, 0.013075141, -0.052312399,
0.052374545, 0.017044802, -0.14227364, 0.26541378, 0.68194015, 0.26541378,
-0.14227364, 0.017044802, 0.052374545, -0.052312399, 0.013075141, 0.018740745,
-0.039817952, 0.0076925293
};
Die, für den C-Code notwendige, Filterstruktur kann ebenfalls dem Designer entnommen werden, wobei die angezeigten Koeffizienten gerundet werden:
Für die Umsetzung des Filters werden also n Elemente benötigt, die jeweils den vorangegangenen Wert mit einem Koeffizienten multiplizieren und die einzelnen Produkte aufsummieren. Der Eingangswert wird dann um einen Takt verzögert (Z-1) und an das nächste Element weitergegeben.
static data_t ShiftRegRight[LENGTH];
static data_t ShiftRegLeft[LENGTH];
acc_t AccRight = 0x00;
acc_t AccLeft = 0x00;
data_t DataRight;
data_t DataLeft;
if(Enable == true)
{
Shift_Accum_Loop: for(int i = (LENGTH - 1); i >= 0; i--)
{
if(i == 0)
{
ShiftRegRight[0] = DataIn & 0x0000FFFF;
ShiftRegLeft[0] = (DataIn & 0xFFFF0000) >> 0x10;
DataRight = DataIn & 0x0000FFFF;
DataLeft = (DataIn & 0xFFFF0000) >> 0x10;
}
else
{
ShiftRegRight[i] = ShiftRegRight[i - 1];
ShiftRegLeft[i] = ShiftRegLeft[i - 1];
DataRight = ShiftRegRight[i];
DataLeft = ShiftRegLeft[i];
}
AccRight += DataRight * Coefficients[i];
AccLeft += DataLeft * Coefficients[i];
}
*DataOut = ((AccLeft.range() >> 0x20) << 0x10) | (AccRight.range() >> 0x20);
}
else
{
*DataOut = DataIn;
}
Für die verzögerten Elemente wird ein Array vom Typ data_t verwendet. Dieses Array bildet dann eine Kette aus Schieberegister. Bei jedem Schleifendurchlauf werden die Daten in dem Schieberegister mit den Koeffizienten verrechnet und die Ausgangssumme bestimmt. Anschließend werden die Werte um eine Stelle verschoben und ein neuer Wert in das erste Schieberegister eingelesen.
Achtung:
Durch den Code wird eine Hardware beschrieben, kein Programm! Die for-Schleife kann somit nacheinander (Loop Pipelining) oder parallel (Loop Unrolling) ausgeführt werden. Je nachdem welche Methode gewählt wird, verringern sich die Durchlaufzeit (Unroll) oder die benötigten Ressourcen (Pipelining) des Filters.
Bevor der Code zu einen IP-Block für das Hardwaredesign kompiliert werden kann, müssen noch ein paar Direktiven eingefügt werden, damit die High-Level Synthese weiß, wie sie z. B. Schleifen auflösen oder ob die Funktionsparameter bestimmte Protokolle besitzen sollen.
Die Direktiven können entweder im Quellcode oder in einer separaten TCL-Datei eingetragen werden. Xilinx empfiehlt die zweite Variante, da auf diese Weise verschiedene Direktiven für verschiedene Testbenches genutzt werden können. Für den Filter werden die folgenden Direktiven deklariert:
set_directive_interface -mode axis -register -register_mode both -depth 1 "Filter" DataIn set_directive_interface -mode axis -register -register_mode both -depth 1 "Filter" DataOut set_directive_interface -mode ap_ctrl_none "Filter"
Über die ersten beiden Direktiven werden die Funktionsparameter DataIn und DataOut mit einem AXI-Stream Interface ausgestattet. Mit Hilfe der letzten Direktive wird das Kontrollinterface für den IP-Block festgelegt. Da in diesem Beispiel lediglich eine Takt- und eine Reset-Leitung genutzt werden soll, kann das Interface über den Parameter ap_ctrl_none entfernt werden. Für das Enable-Signal müssen keine Direktiven festgelegt werden, da dieses Signal ein einfacher Eingang sein soll. Jetzt kann der IP-Block über die Schaltfläche C Synthesis synthetisiert werden.
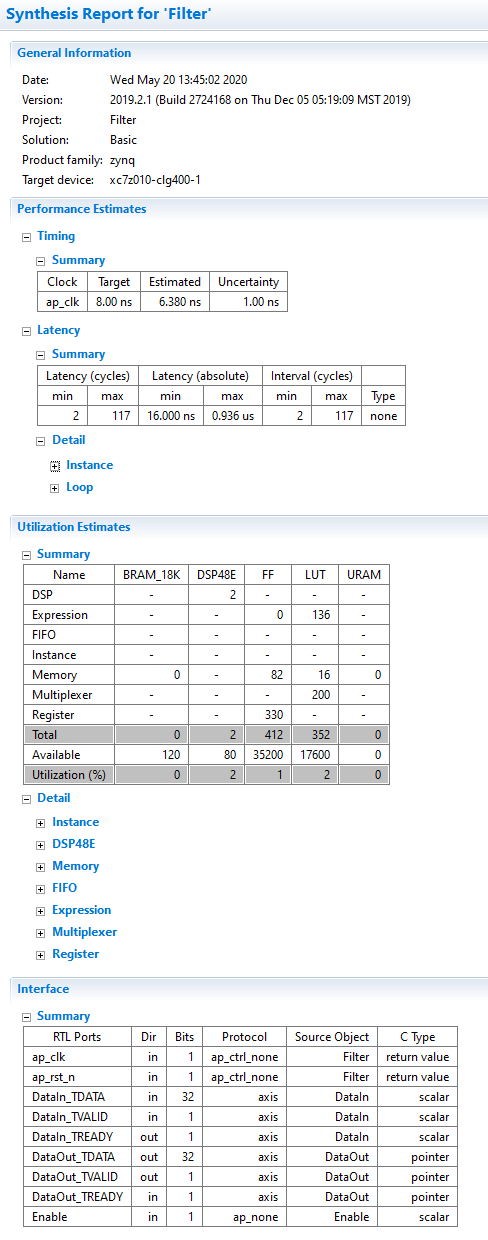
Wenn die Synthese erfolgreich war, erhält man einen Bericht mit einer (geschätzten) Ressourcenbelegung im FPGA, sowie einer Timing-Analyse.
Wenn alles korrekt eingestellt wurde, werden zwei DSP-Blöcke (je einer für einen Audiokanal) genutzt. Für die Steuerung des Blocks sind zwei Eingänge mit den Namen ap_clk und ap_rst_n, sowie das Enable-Signal und für die Ein- und Ausgabe der Daten zwei AXI-Stream Interfaces erzeugt worden.
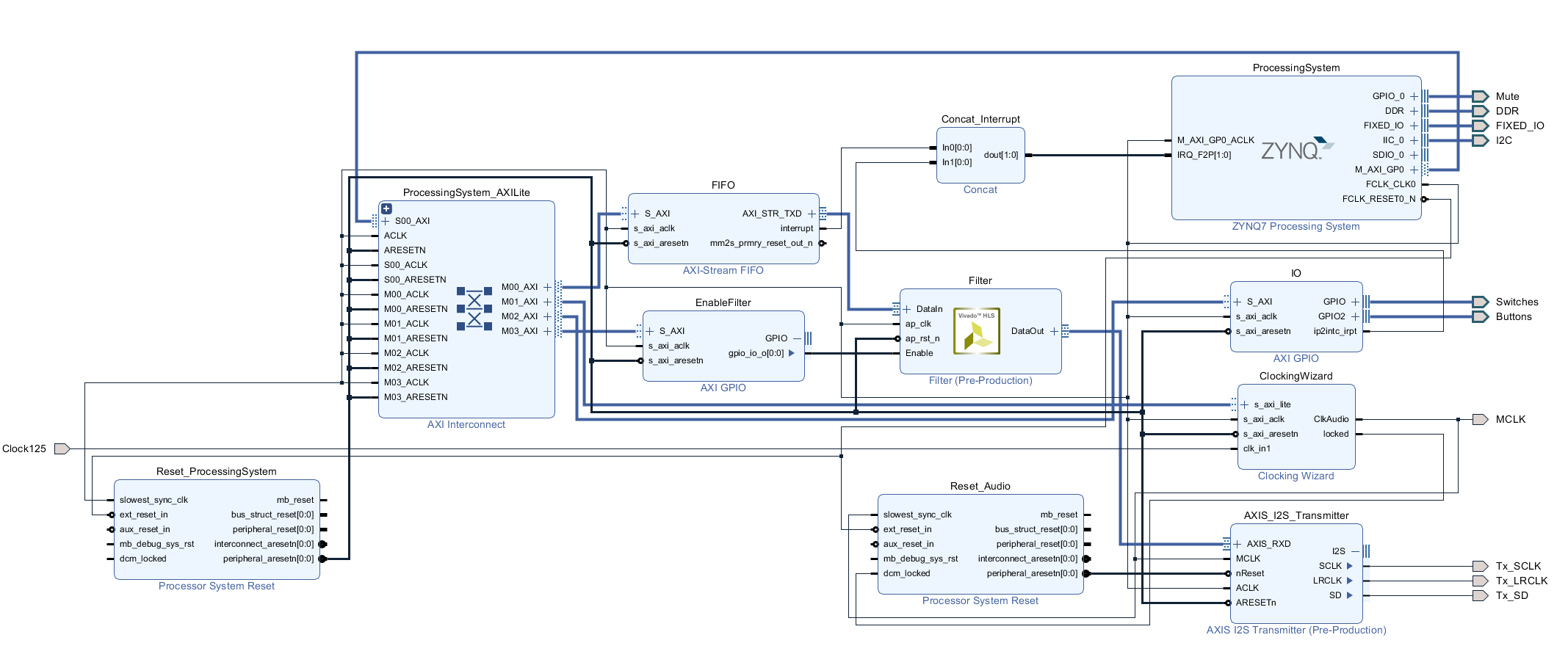
Wenn alles korrekt ist, wird das Design über die Schaltfläche Export RTL in einen IP-Block exportiert und in das Blockdesign eingefügt. Für die Aktivierung und Deaktivierung des Filters verwende ich einen weiteren AXI-GPIO IP-Block.
Zum Schluss wird das Blockdesign erstellt und dann kann auch schon die Software angepasst werden.
Für die Software verwende ich die bereits erstellte Software aus dem SSM2603-Teil dieses Tutorials und erweitere sie um den eingefügten GPIO-Block. Zuerst wird die Funktion AudioPlayer_InitGPIO angepasst um den IP-Block vor der ersten Nutzung zu initialisieren:
static u32 AudioPlayer_InitGPIO(void)
{
xil_printf("[INFO] Looking for GPIO configuration...\r\n");
_Mute_ConfigPtr = XGpioPs_LookupConfig(XPAR_PS7_GPIO_0_DEVICE_ID);
_IO_ConfigPtr = XGpio_LookupConfig(XPAR_IO_DEVICE_ID);
_Filter_ConfigPtr = XGpio_LookupConfig(XPAR_ENABLEFILTER_DEVICE_ID);
if((_Mute_ConfigPtr == NULL) || (_IO_ConfigPtr == NULL) || (_Filter_ConfigPtr == NULL))
{
xil_printf("[ERROR] Invalid GPIO configuration!\r\n");
return XST_FAILURE;
}
xil_printf("[INFO] Initialize GPIO...\r\n");
if((XGpioPs_CfgInitialize(&_Mute, _Mute_ConfigPtr, _Mute_ConfigPtr->BaseAddr) != XST_SUCCESS) || (XGpio_CfgInitialize(&_IO, _IO_ConfigPtr, _IO_ConfigPtr->BaseAddress) != XST_SUCCESS) || (XGpio_CfgInitialize(&_Filter, _Filter_ConfigPtr, _Filter_ConfigPtr->BaseAddress) != XST_SUCCESS))
{
xil_printf("[ERROR] GPIO initialization failed!\n\r");
return XST_FAILURE;
}
...
}
Über den GPIO-Interrupthandler wird der AXI-GPIO Block dann ausgelesen und der Filter geschaltet:
static void AudioPlayer_GpioHandler(void* CallbackRef)
{
XGpio* InstancePtr = (XGpio*)CallbackRef;
u32 Status = XGpio_InterruptGetStatus(InstancePtr);
if(Status & XGPIO_IR_CH1_MASK)
{
if(Status & XGPIO_IR_CH1_MASK)
{
if(XGpio_DiscreteRead(&_IO, 1) & 0x01)
{
AudioPlayer_Mute(true);
}
else
{
AudioPlayer_Mute(false);
}
if(XGpio_DiscreteRead(&_IO, 1) & 0x02)
{
AudioPlayer_EnableFilter(true);
}
else
{
AudioPlayer_EnableFilter(false);
}
}
}
...
}
void AudioPlayer_EnableFilter(const bool Enable)
{
XGpio_DiscreteWrite(&_Filter, 1, Enable);
}
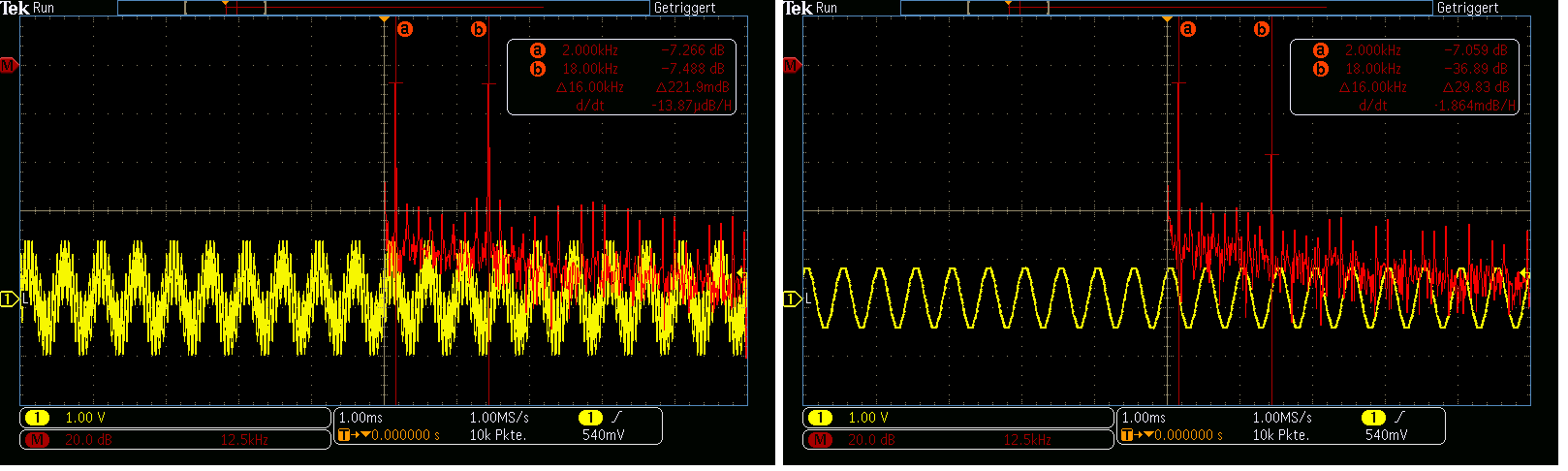
Die fertige Software wird nun auf den Prozessor überspielt und ausgeführt werden. Sobald der Filter eingeschaltet wird, werden die hochfrequenten Signalanteile bei 18 kHz gedämpft.
Damit wäre der Audiofilter fertig. Die Dämpfung beträgt ungefähr -30 dB und stimmt ziemlich genau mit dem Wert aus dem Filter-Tool überein. Selbstverständlich kann das Design noch angepasst / verbessert werden, um z. B. die Koeffizienten dynamisch zu laden. Aber für den ersten Wurf kann sich das Ergebnis durchaus sehen lassen.
Als nächstes wollen wir uns mit dem Empfang von Audiodaten über I2S beschäftigen. Doch dazu wird erst einmal ein passender Empfänger benötigt…
→ Zurück




Schreibe einen Kommentar