In diesem Artikel möchte ich die Implementierung eines genetischen Algorithmus für das Problem des Handlungsreisenden vorstellen. Das Ziel besteht darin, dass der Algorithmus den kürzesten Weg zwischen beliebig vielen Punkten (z. B. Städte) sucht, ohne das ein Punkt (mit Ausnahme des Startpunktes) mehr als einmal besucht wird.
Was ist ein „genetischen Algorithmus“?:
Unter einem evolutionären Algorithmus versteht man einen Algorithmus, der ähnlich funktioniert wie die natürliche Evolution eines Lebewesens. Diese Algorithmen werden für die Optimierung, bzw. für die Suche nach einer Lösung bei einem gegebenen Problem eingesetzt. In der Regel wird ein Merkmal des gegebenen Problems bestimmt, welches optimiert werden soll.
Der Algorithmus versucht dann durch zufällige Veränderungen einer Population das Merkmal zu optimieren. Dies geschieht durch Mutationen des Merkmals. Ganz wie in der Natur werden nur die besten Merkmale an die nächste Population weitergegeben. Ein genetischer Algorithmus besteht immer aus den selben Abläufen:
- Initialisierung – Es wird eine erste Population mit Merkmalen erzeugt (meistens mit zufälligen Werten)
- Evaluierung – Die einzelnen Individuen der Population werden hinsichtlich ihrer Güte untersucht. Diese Güte wird anschließend in eine Fitness umgerechnet
- Selektion – Aus der Population werden Individuen für eine Rekombination ausgewählt
- Rekombination – Zwei Eltern (ausgewählten Individuen) werden miteinander kombiniert und bilden Nachfahren
- Mutation – Zufällige Nachfahren mutieren
- Evaluierung – Es wird die Fitness der neuen Generation bestimmt
- Wiederholung ab Schritt 3
Der Ablauf wird so lange wiederholt bis ein bestimmtes Abbruchkriterium (z. B. eine Anzahl von Durchläufen) erreicht wurde. Das Ergebnis des Algorithmus ist dann die „stärkste“ Generation, die das gegebene Problem am optimalsten löst.
Implementierung der Lösung
Gegeben ist die folgende Ausgangssituation:
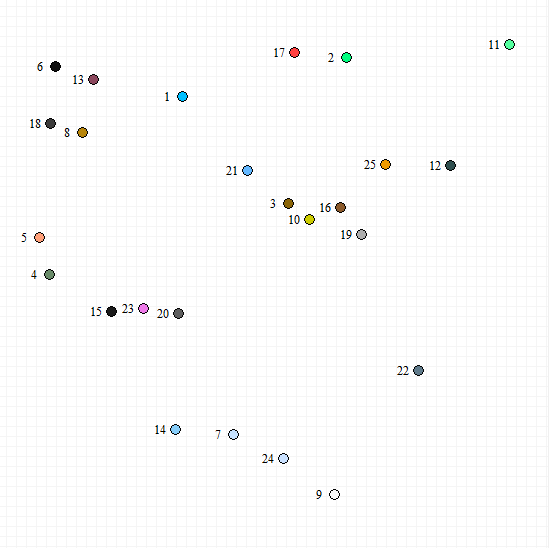
Es sollen eine gegebene Menge Städte (hier 25 Stück) auf dem kürzesten Gesamtweg besucht werden. Am Ende der Tour soll in die Anfangsstadt zurückgekehrt werden. Der Startpunkt kann beliebig gewählt werden, aber es darf jede Stadt nur einmal besucht werden. Als Stadtkarte sei eine zufällige Anordnung von Punkten gegeben:
Die Städte werden durch eine City-Klasse beschrieben. Diese Klasse beinhaltet zwei Properties für die Position der Stadt als x- und y-Koordinaten, sowie eine Methode zum Berechnen der euklidischen Distanz zwischen zwei verschiedenen Städten.
import numpy
class City(object):
def __init__(self, x, y, name):
self.__x = x
self.__y = y
self.__name = name
@property
def x(self):
return self.__x
@property
def y(self):
return self.__y
@property
def name(self):
return self.__name
def Distance(self, Neighbor):
Distance_x = abs(self.__x - Neighbor.x)
Distance_y = abs(self.__y - Neighbor.y)
return numpy.sqrt((Distance_x ** 2) + (Distance_y ** 2))
def __repr__(self):
return "({}, {}) - {}".format(self.__x, self.__y, self.__name)
Für den Algorithmus wird zudem ein Optimierungsmerkmal benötigt. Mit diesem Optimierungsmerkmal wird die Fitness ausgerechnet, die bestimmt wie gut der jeweilige Durchlauf ist.
In diesem Beispiel stellt die Gesamtdistanz der Städtetour das Optimierungsmerkmal dar. Der Algorithmus versucht während der Evolution eine hohe Fitness zu erreichen, wobei eine große Distanz eine schlechte Fitness und eine kleine Distanz eine große Fitness ergeben soll. Die Fitness berechnet sich in diesem Beispiel also aus der inversen Fitness.
class Fitness(object):
def __init__(self, TourList):
self.__TourList = TourList
self.__Distance = 0
self.__Fitness = 0
def __TourDistance(self):
if(self.__Distance == 0):
PathDistance = 0
for I in range(0, len(self.__TourList)):
FromCity = self.__TourList[I]
ToCity = None
if((I + 1) < len(self.__TourList)):
ToCity = self.__TourList[I + 1]
else:
ToCity = self.__TourList[0]
PathDistance += FromCity.Distance(ToCity)
self.__Distance = PathDistance
return self.__Distance
def TourFitness(self):
if(self.__Fitness == 0):
self.__Fitness = 1.0 / float(self.__TourDistance())
return self.__Fitness
Nun wird eine Startpopulation benötigt und für die Startpopulation werden Städte, bzw. deren Koordinaten benötigt. Diese Städte werden zufällig erzeugt und gespeichert.
for Index in range(0, self.__CityCount.get()): x = int(random.random() * self.__Width) y = int(random.random() * self.__Height) self.__Cities.append(City(x = x, y = y, name = str(Index + 1)))
Mit diesen Städten können nun die erste Population entwickelt werden. Hierzu wird eine zufällige Besuchsreihenfolge der Städte erstellt und in einer Liste gespeichert.
def CreateRandomRoutes(self): return random.sample(self.__Cities, len(self.__Cities))
Dieser ganze Vorgang wird 100x wiederholt, wodurch sich die erste Population aus 100 verschiedenen Anordnungen von Städten bildet.
def CreatePopulation(self, Size): self.__Population = list() for _ in range(0, Size): self.__Population.append(self.CreateRandomRoutes())
Diese Population wird nun hinsichtlich ihrer Fitness untersucht. Dazu wird von jedem Individuum, also von jeder zufälligen Anordnung der Städte, die Gesamtstrecke berechnet. Aus den Gesamtstrecken ergeben sich dann die Fitnesswerte der Individuuen. Die einzelnen Fitnesswerte werden mit einem entsprechenden Index auf das jeweilige Individuum in einem Dictionary abgespeichert. Abschließend wird das Dictionary bzgl. der Fitnesswerte sortiert.
def RankPopulation(self):
FitnessResults = dict()
for I in range(0, len(self.__Population)):
FitnessResults.update( {I : Fitness(self.__Population[I]).TourFitness()} )
return sorted(FitnessResults.items(), key = operator.itemgetter(1), reverse = True)
Mit diesen Fitnesswerten wird nun die erste Selektion vorgenommen um eine neue Population zu bilden. Die neue Population beinhaltet ausschließlich Individuen der Quellpopulation, aber zwangsweise nicht alle. Es kann somit vorkommen, dass ein Individuum mehr als als einmal in der Selektion auftaucht. Biologisch entspricht das der Tatsache, dass ein Lebewesen mit mehreren unterschiedlichen Lebewesen Nachkommen zeugen kann.
Als Selektionsmerkmal wird zum einen Elitarismus genutzt, wodurch die n besten Individuen der Population automatisch selektiert werden.
for I in range(0, EliteSize): MatingPool.append(self.__Population[RankedPopulation[I][0]])
Und zum anderen wird eine Fitness proportionate selection verwendet, bei der die Selektionswahrscheinlichkeit durch die relative Fitness bzgl. der Population berechnet wird. Dieses Verfahren sorgt dafür, dass Individuen mit einer sehr geringen Fitness mit in die Selektion aufgenommen werden (wenn auch mit einer kleineren Chance). Die selektierten Individuen bilden den sogenannten Paarungspool (Mating pool).
MatingPool = list() Frame = pandas.DataFrame(numpy.array(RankedPopulation), columns = ["Population", "Fitness"]) Frame["RelativeFitness"] = Frame.Fitness.cumsum() / Frame.Fitness.sum() for I in range(0, EliteSize): MatingPool.append(self.__Population[RankedPopulation[I][0]]) for _ in range(0, len(RankedPopulation) - EliteSize): Pick = random.random() for I in range(0, len(RankedPopulation)): if(Pick <= Frame.iat[I, 2]): MatingPool.append(self.__Population[RankedPopulation[I][0]]) break
Dieser Paarungspool wird nun genutzt um Nachkommen zu bilden. Dazu werden die neue Population gemischt und es werden die n besten Individuen. Diese Individuen bilden automatisch die nächsten Nachkommen.
Children = list() for I in range(0, EliteSize): Children.append(MatingPool[I])
Der Rest der Population bilden die Elternteile. Dabei werden iterativ über die Population je zwei Individuen als Vater und als Mutter deklariert, wobei das I-te Individuum den Vater und das len(Population) – I – 1-te die Mutter darstellt. Nach len(Population) / 2 Zyklen tauschen Vater und Mutter die Positionen.
RandomPool= random.sample(MatingPool, len(MatingPool)) for I in range(0, len(MatingPool) - EliteSize): Child = self.Breed(RandomPool[I], RandomPool[len(MatingPool) - I - 1]) Children.append(Child)
Beide Eltern erzeugen anschließend die Nachkommen. Auch hier Ähnlich wie in der Biologie werden auch hier bei der Nachkommensbildung unterschiedlich viele Merkmale beider Elternteile verwendet um einen Nachkommen zu zeugen.
def Breed(self, Father, Mother): ChildFather = list() ChildMother = list() GenA = int(random.random() * len(Father)) GenB = int(random.random() * len(Mother)) for I in range(min(GenA, GenB), max(GenA, GenB)): ChildFather.append(Father[I]) ChildMother = [Item for Item in Mother if Item not in ChildFather] return = ChildFather + ChildMother
Damit ist die Nachkommensbildung abgeschlossen und eine neue Generation der ursprünglichen Population steht bereit.
In der Genetik kommt es allerdings vor, dass zufällige Individuen mutieren und sich verändern. Wenn diese Veränderungen im Sinne des Individuums positiv sind, vererbt es diese Mutationen unter Umständen weiter, wodurch die Nachkommen einen Vorteil gegenüber den Nachkommen von nicht mutierten Individuuen haben. Bisher stellt der Algorithmus eine Welt ohne Evolution dar. Während der Mutation verändern sich einzelne Merkmale eines Individuums. Dies ist in diesem Fall nicht möglich, da die Position der Städte nicht verändert werden kann. Stattdessen wird die Position einer Stadt mit der Position einer anderen zufälligen Stadt getauscht.
def Mutate(self, Individual, MutationRate): for Swapped in range(len(Individual)): if(random.random() < MutationRate): SwapWith = int(random.random() * len(Individual)) Temp1 = Individual[Swapped] Temp2 = Individual[SwapWith] Individual[Swapped] = Temp2 Individual[SwapWith] = Temp1 return Individual
Die Mutation wird nun auf die komplette Population angewandt, sodass jedes Individuum der Population die gleiche Chance erhält zu mutieren.
def MutatePopulation(self, Population, MutationRate): MutatedPopulation = list() for I in range(0, len(Population)): MutatedPopulation.append(self.Mutate(Population[I], MutationRate)) self.__Population = MutatedPopulation
Als Resultat erhält man eine neue Population, die über eine einer besseren Gesamtfitness verfügt als die Ausgangspopulation. Durch mehrmaliges Wiederholen der Vorgänge kann die Fitness bis zu einem bestimmten Wert immer weiter verbessert werden.
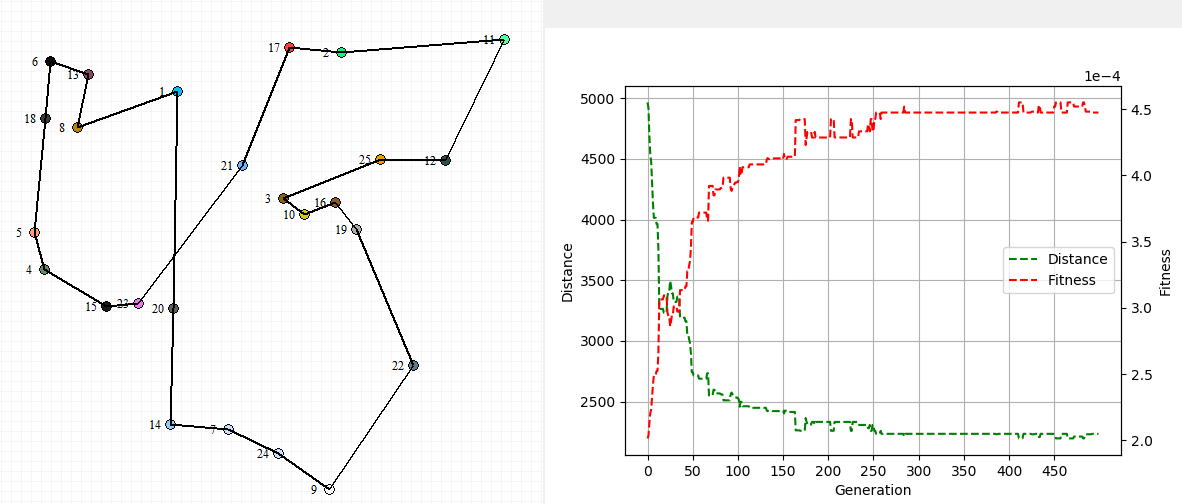
Das Ergebnis des Algorithmus ist eine optimierte Besuchsreihenfolge der Städte (hier als Beispiel für 500 Zyklen).
Der Ergebnisplot auf der rechten Seite zeigt deutlich, dass sich das Ergebnis nach 250 Generationen nicht mehr stark verbessert hat. Meine Implementierung optimiert ggf. zu lange, da sie lediglich einen Zähler als Abbruchvariante verwendet. Hier kann der Algorithmus noch optimiert werden, indem er die Optimierung z. B. beim erreichen einer Mindestfitness abbricht. Die bessere Variante ist allerdings, dass der Algorithmus sich die letzten n Fitnesswerte anschaut und nur abbricht, wenn die Fitness näherungsweise konstant bleibt.
Das komplette Projekt (mit einer schönen Tk-GUI) ist, wie immer, in meinem GitHub-Repository zu finden.
Viele Grüße
Daniel



Schreibe einen Kommentar